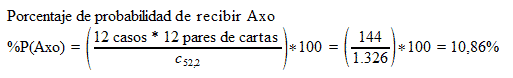Se llama cartas offsuited a las combinaciones de dos cartas de rangos y palos distintos. Para avanzar en los cálculos de cartas offsuited, en primer lugar hemos de saber cuántas combinaciones puede haber de dos cartas distintas concretas; por ejemplo, AKso. Para ello, podemos utilizar la fórmula de la distribución multihipergeométrica:
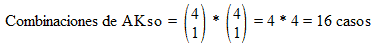
La fórmula es fácil de entender:
- El primer 4 sobre 1 quiere decir que una de las dos cartas ha de ser un as.
- El segundo 4 sobre 1 quiere decir que la otra carta debe ser un rey.
Por tanto, hay 16 posibles combinaciones de dos cartas concretas (suited+offsuited). Si queremos saber cuántas hay offsuited, simplemente hemos de restar a las 16 totales las 4 combinaciones de cartas del mismo palo.
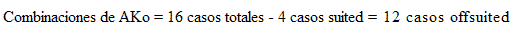
Por tanto, hay 12 posibles combinaciones de dos cartas offsuited concretas. Entonces, ¿cuál es la probabilidad de que el croupier nos dé AKo en el pre-flop? Podemos calcular dicho porcentaje dividiendo los 12 casos posibles por el total de combinaciones de dos cartas de las 52 de la baraja:
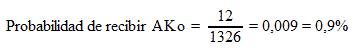
Como puedes ver, la probabilidad de recibir AKo es del 0,9%.
Veamos más cálculos de cartas offsuited. ¿Cuál sería la probabilidad de recibir dos cartas offsuited cualesquiera?
Como calculamos en la página de cartas pre-flop, hay 78 combinaciones de pares de cartas genéricos de distinto rango en la baraja. Por tanto, si hay 12 casos por combinación, el total de combinaciones del patrón XYo será de 78 * 12 = 936 pares de cartas offsuited. Podemos calcular la probabilidad de que el crouper nos dé dos cartas offsuited cualquiera.
En el 70,59% de las manos recibirás cartas de distintos rangos y palos.
Por último, vamos a calcular la probabilidad de que el croupier te dé un as y otra carta, ambas de distintos palos (Axo). Sabemos que hay 12 casos por combinación de cartas y que el as puede ir acompañado por cartas de los restantes 12 rangos de la baraja. También conocemos el número de combinaciones de 52 cartas tomadas de 2 en 2. Por tanto, la probabilidad de recibir Axo sería del 10,86%, tal como podemos ver en la siguiente fórmula: